Prečo to funguje?

Ukážeme si, že robotovo prehľadávanie má dobré vlastnosti:

Po konečnom počte krokov skončí.

Po konečnom počte krokov skončí. Vždy, keď robot vojde do nového zeleného vrcholu, hneď potom ho prefarbí na červeno. Keďže každý vrchol sa dá prefarbiť iba raz, v grafe s n vrcholmi môže robot urobiť nanajvýš n krokov typu a) (v skutočnosti $n−1$, lebo v jednom zelenom vrchole začína).

Okrem toho robí robot ešte kroky typu b), keď sa z červeného vcholu vracia po hrane, po ktorej sa doň prvý raz dostal. Dá sa ukázať, že aj týchto krokov bude konečne veľa. Predstavme si, že robot by vždy, keď prefarbuje vrchol na červeno, napísal do tohto vrcholu ešte jedno číslo (budeme ho volať hĺbka vrcholu), nasledovným spôsobom:

• Do štartovacieho vrcholu napíše číslo 0.
• Vždy, keď vojde do nového zeleného vrcholu, napíše doň o 1 väčšie číslo než je vo vrchole, odkiaľ prišiel.

Počas robotovej prechádzky grafom môžeme sledovať, v akej je robot hĺbke -- teda akú hĺbku má vrchol, v ktorom sa robot práve nachádza. Vždy, keď robot urobí krok do zeleného vrcholu (a prefarbí ho), hĺbka robota stúpne o 1. Vždy, keď sa robot vracia z červeného vrcholu hranou, ktorou prišiel, jeho hĺbka klesne o 1. Hĺbka pritom v každom momente bude nezáporná (lebo záporné čísla nám nemajú ako vzniknúť). Keďže robot začína v hĺbke 0 a urobí nanajvýš n krokov, v ktorých jeho hĺbka stúpne (krokov, kde vojde do zeleného vrcholu), nemôže urobiť viac než $n$ krokov, pri ktorých jeho hĺbka klesne (inak by skončil v zápornej hĺbke). To znamená, že robot zaručene skončí po nanajvýš $2n$ krokoch.

Ofarbí na červeno všetky vrcholy, do ktorých sa dá dostať z vrcholu $S$

Najprv si všimnime, že robotova prechádzka má jednu zaujímavú vlastnosť: z každého vrcholu, do ktorého robot vojde ako do zeleného, sa niekedy neskôr vráti po hrane, ktorou doň prvý raz prišiel.

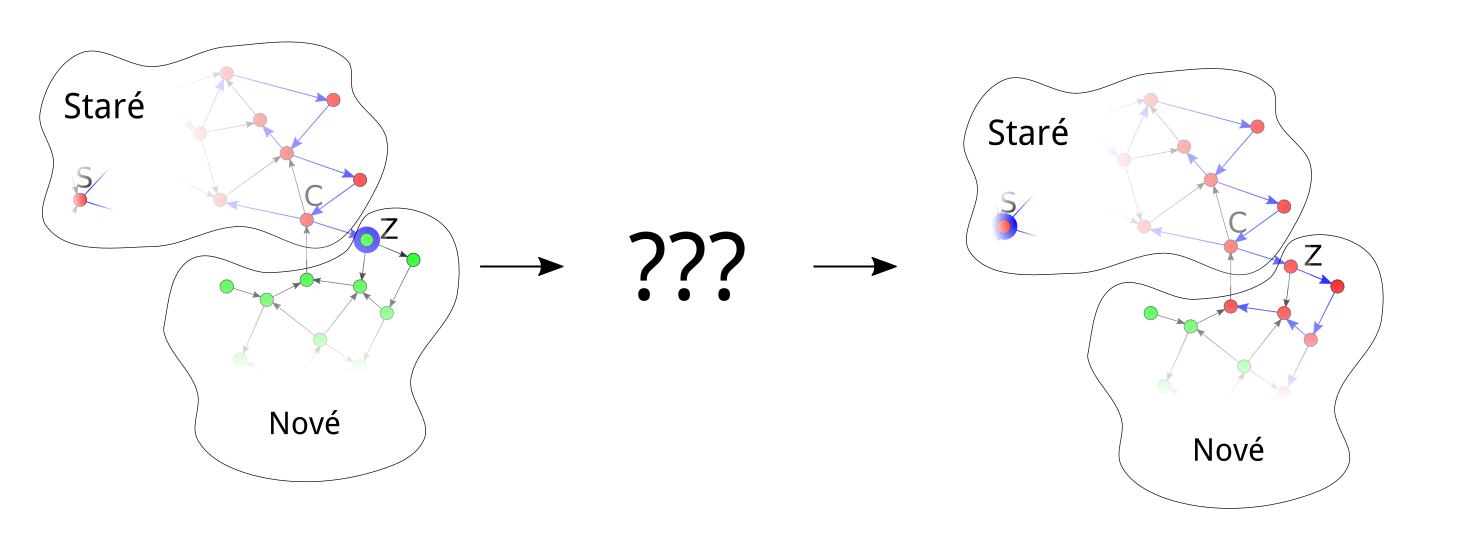
Prečo je to tak? Predstavme si situáciu, keď robot prešiel z nejakého červeného vrcholu $C$ do zeleného vrcholu $Z$ (ale ešte ho neprefarbil). Vrcholy, ktoré sú v tomto momente červené, budeme volať staré a vrcholy, ktoré sú v tomto momente zelené, budeme volať nové. Robot je teda momentálne vo vrchole $Z$, ktorý je nový. Na konci algoritmu však bude vo vrchole $S$ (lebo len tam sa môže vypnúť), ktorý je zaručene starý. To znamená, že niekedy medzi súčasným okamihom a koncom algoritmu bude musieť prejsť z nejakého nového vrcholu do nejakého starého vrcholu. Keď sa toto stane prvý raz, určite to bude krokom typu b), keďže kroky typu a) musia ísť do zelených vrcholov a všetky staré vrcholy sú už teraz červené. V tomto kroku sa teda robot bude z nejakého nového vrcholu vracať po hrane, ktorou ho objavil, naspäť do nejakého starého vrcholu. Od momentu, keď vošiel do vrcholu $Z$, však ešte v žiadnom starom vrchole nebol. To znamená, že všetky nové vrcholy (okrem $Z$), ktoré medzičasom prefarbil, musel objaviť len z iných nových vrcholov. Jediný možný spôsob, ako sa mohol vrátiť na starý vrchol je teda ten, že sa vrátil zo $Z$ na $C$.

Nakoniec si ešte stačí uvedomiť, že ako vrchol $Z$ mohol v predchádzajúcej úvahe vystupovať ľubovoľný vrchol (okrem $S$), ktorý robot počas svojej prechádzky objavil a prefarbil. To znamená, že z každého vrcholu, ktorý robot objaví, sa niekedy neskôr vráti po hrane, ktorou doň prvý raz vošiel.

Poďme teraz ukázať pôvodné tvrdenie (že robot objaví všetky vrcholy dosiahnuteľné z $S$). Predstavme si, že by to tak nebolo, teda že by sa v grafe dal nájsť bol vrchol $D$, ktorý je dosiahnuteľný z $S$, ale robot ho neobjavil. Vrchol D má byť dosiahnuteľný, teda v grafe má existovať cesta z $S$ do $D$ Posledný vrchol na tejto ceste, ktorý robot ešte objavil (a prefarbil na červeno) označme O a prvý vrchol, ktorý už neobjavil, označme $N$. Z vrcholu O sa teda po hrane dá dostať do $N$.

Vieme, že v nejakom momente robot vošiel do vrcholu O krokom typu a) (resp. ak O je totožný s $S$, tak v ňom začal na začiatku). Ukázali sme už, že potom z neho musel niekedy neskôr odísť krokom typu b) (v prípade, že $O=S$, sa v ňom musel na konci vypnúť). To ale znamená, že tesne pred týmto krokom typu b) (alebo vypnutím) bol robot vo vrchole O a nemohol sa z neho po hrane dostať do žiadneho zeleného vrcholu. Čo však nesedí s tým, že z O sa dá ísť po hrane do vrcholu $N$, ktorý zostal až do konca zelený. Celá táto situácia je teda nemožná, čiže robot naozaj objaví všetky vrcholy, do ktorých sa z $S$ dá dostať.

Neprefarbí (ani nenavštívi) už nič iné.

Robot začína vo vrchole $S$, ktorý zjavne je dosiahnuteľný z $S$. Ak by mal počas prechádzky vojsť do nedosiahnuteľného vrcholu, niekedy by sa to muselo stať prvý raz. Určite sa to nemôže stať krokom typu b), lebo takýmto krokom sa robot vracia na vrchol, kde už niekedy bol a doteraz bol iba na dosiahnuteľných vrcholoch. Nemôže sa to stať ani krokom typu a), lebo z dosiahnuteľného vrcholu sa po hrane grafu dá dostať iba do dosiahnuteľného. To znamená, že robot sa nemá ako dostať do nedosiahnuteľného vrcholu.