Binárna halda
Tak, a sme tu. Po všetkej príprave si konečne ideme vyrobiť konkrétnu vlastnú haldu. A určite už tušíte, ako na to pôjdeme: naša halda (odborne nazývaná binárna halda) bude mať tvar takmer úplného binárneho stromu.
Obrázok 5: Binárna maximová halda obsahujúca 10 prvkov.
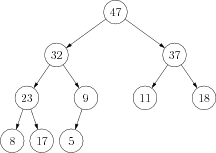
Veľkou výhodou binárnej haldy je, že ju vieme ľahko implementovať bez použitia referencií alebo pointrov. Stačí nám jedno dostatočne veľké pole. Haldu doň uložíme "po riadkoch". Teda na začiatku poľa bude uložený koreň, za ním zľava doprava jeho synovia, za nimi zľava doprava ich synovia, a tak ďalej.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| prvok | 47 | 32 | 37 | 23 | 9 | 11 | 18 | 8 | 17 | 5 |
Všimnite si, že $n$-prvková binárna halda nám zaberá presne prvých $n$ pozícii v poli. Ak majú prvky v poli indexy $0$ až $n−1$, tak platia nasledovné vlastnosti:
- Otec vrcholu s indexom $x$ má index $\lfloor (x−1)/2 \rfloor$.
- Synovia tohoto vrcholu majú indexy $2x+1$ a $2x+2$ .
Ku každému vrcholu teda vieme jeho otca aj prípadných synov nájsť v konštantnom čase. Vďaka tomuto nepotrebujeme žiadne pointre, aj bez nich vieme priamo s poľom pracovať tak, ako by sme pracovali s haldou reprezentovanou ako strom.