Jeden možný dobrý tvar haldy

Z odhadov časovej zložitosti je jasné, ako by mala dobrá halda vyzerať: mala by mať malú hĺbku a mala by zároveň mať malé stupne vrcholov. Existujú rôzne typy stromov, ktoré toto spĺňajú. Asi najjednoduchším typom sú takzvané takmer úplné binárne stromy.

Pripomeňme si, že v binárnom strome môže každý vrchol mať nanajvýš dvoch synov -- jedného ľavého a jedného pravého. A tiež si pripomeňme, že hĺbka vrcholu je definovaná ako počet hrán na ceste z neho do koreňa.

Binárny strom môžeme rozdeliť na úrovne. Úroveň $k$ tvoria všetky vrcholy, ktoré majú hĺbku $k$. Všimnime si, že na úrovni $k$ môžeme mať nanajvýš $2k$ vrcholov. (Na úrovni $0$ je len koreň, ten má nanajvýš $2$ synov ktorí tvoria úroveň $1$, každý z nich má nanajvýš $2$ synov ktorí spolu tvoria úroveň $2$, atď.)

Binárny strom voláme úplný, ak je každá jeho úroveň buď prázdna alebo úplne plná -- inými slovami, ak má každý vrchol v každej úrovni okrem poslednej práve dvoch synov. Úplný binárny strom hĺbky k má teda presne $1+2^1+ \dots +2^{k−1}+2^k=2^{k+1}−1$ vrcholov, a z nich $2^k$ sú listy.

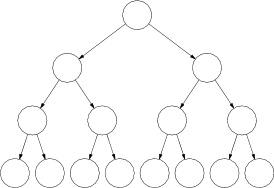
Zjavne pre skoro žiadne $n$ neexistuje úplný binárny strom s $n$ vrcholmi. Budeme sa teda musieť uspokojiť so stromami, ktoré sa na úplné dostatočne podobajú.

Takmer úplný binárny strom je taký binárny strom, ktorý má všetky úrovne okrem poslednej plné, a v poslednej sú všetky vrcholy natoľko vľavo, nakoľko sa to pri ich počte dá.

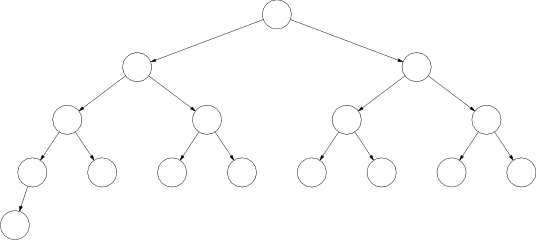
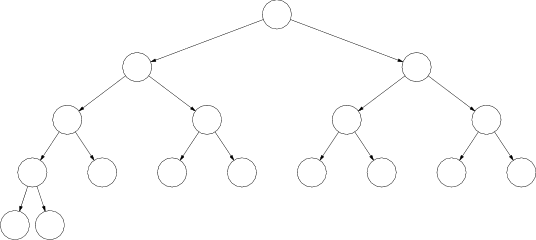
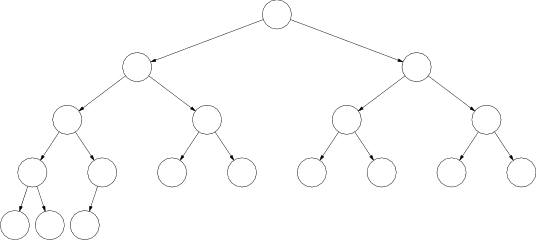
Zjavne pre každé $n$ existuje práve jeden takmer úplný binárny strom s $n$ vrcholmi. Ich konštrukciu môžeme popísať aj takto: Takmer úplný strom s $n>1$ vrcholmi zostrojíme z takmer úplného stromu s $n−1$ vrcholmi tak, že nájdeme najmenšiu úroveň, do ktorej sa dá pridať vrchol, a pridáme ho do nej na najľavejšie možné miesto.

Tiež si všimnite, že pre každé $n$ z množiny $2^k, 2^{k+1},\dots,2^{k+1}−1$ má $n$-vrcholový takmer úplný binárny strom hĺbku $k$. Toto isté môžeme povedať aj nasledovne: Takmer úplný binárny strom s $n$ vrcholmi má hĺbku $\lfloor log2n \rfloor$.