Všeobecná maximová halda

Technický detail o prvkoch a prioritách

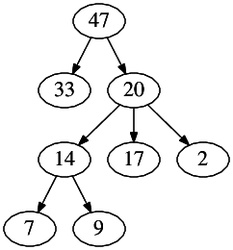
V nasledujúcom texte si pre jednoduchosť budeme zaoberať haldami, v ktorých sú uložené obyčajné prirodzené čísla. Pri skutočnom použití haldy tieto čísla predstavujú priority prvkov uložených v halde. Ak teda napríklad na nižšie uvedenom obrázku vidíte krúžok a v ňom číslo 47, toto číslo môže napríklad predstavovať celý záznam o pacientovi, ktorého priorita v čakárni je 47.

Podobne, keď budeme písať prvok X je väčší ako prvok Y, myslíme tým, že X má väčšiu prioritu.

Všeobecná maximová halda

Maximová halda je zakorenený strom, v ktorom platí: prvok uložený v hociktorom vrchole je väčší alebo rovný ako každý z prvkov uložených v synoch daného vrcholu. Túto vlastnosť budeme volať podmienka haldy.

(Analogicky existuje aj minimová halda, kde uvažujeme opačnú podmienku -- prvok uložený v hociktorom vrchole musí byť menší alebo rovný ako každý z prvkov uložených v jeho synoch.)

Všimnite si, že z podmienky haldy vyplýva, že pre ľubovoľný vrchol $v$ haldy platí, že hodnota v ňom je najväčšia z hodnôt v celom podstrome s koreňom $v$. (Totiž hodnota vo $v$ je väčšia alebo rovná ako hodnoty v jeho synoch, tie sú zase väčšie alebo rovné ako hodnoty v ich synoch, a tak ďalej.)

V koreni haldy je teda nutne vždy uložený najväčší zo všetkých prvkov v halde.

Cvičenie 1

Zamyslite sa teraz nad nasledujúcimi otázkami. Vo všetkých otázkach predpokladáme, že máme maximovú haldu a že prvky v nej sú navzájom rôzne.

• Kde všade sa môže nachádzať druhý najväčší prvok?
• Kde všade sa môže nachádzať tretí najväčší prvok?
• Kde všade sa môže nachádzať najmenší prvok?
• Kde všade sa môže nachádzať druhý najmenší prvok?

Cvičenie 1 -- riešenia

• Druhý najväčší prvok sa musí nachádzať bezprostredne pod koreňom, čiže v jednom z jeho synov.
• Tretí najväčší prvok môže byť tiež synom koreňa, taktiež ale môže byť synom druhého najväčšieho prvku.
• Najmenší prvok musí byť v niektorom z listov.
• Druhý najmenší prvok tiež môže byť v liste, je však ešte jedna možnosť: môže sa stať, že druhý najmenší prvok je vo vrchole, ktorý má práve jedného syna: najmenší prvok.

Všimnite si ten rozdiel medzi množstvom informácie, ktorú máme na rôznych koncoch spektra. O najväčšom prvku vieme presne, kde sa nachádza. Ďalšie veľké prvky sú niekde v jeho bezprostrednom okolí. Na druhej strane o najmenších prvkoch nevieme skoro nič.

(Napríklad v binárnej maximovej halde, ktorá je v texte popísaná neskôr, je 6 možností pre polohu tretieho najväčšieho prvku, zatiaľ čo až zhruba $3n/4$ možností pre polohu tretieho najmenšieho.)