Počítanie 2D prefixových súm
Dvojrozmerné prefixové sumy sa dajú vypočítať v čase lineárnom od veľkosti poľa
(teda v našom prípade $O(nm)$).
Jedna možnosť je spočítať obyčajné jednorozmerné prefixové sumy po riadkoch
a na výslednom poli spočítať prefixové sumy po stĺpcoch
(rozmyslite si, prečo to bude fungovať).
Dá sa to však aj pohodlnejšie, trikom.
Uvedomme si, že (pre x,y>0) číslo t[y][x]
je dosť podobné číslu t[y-1][x], akurát do t[y][x]
zarátavame navyše prvých x čísel y-teho riadka (teda riadka s indexom y-1) poľa d.
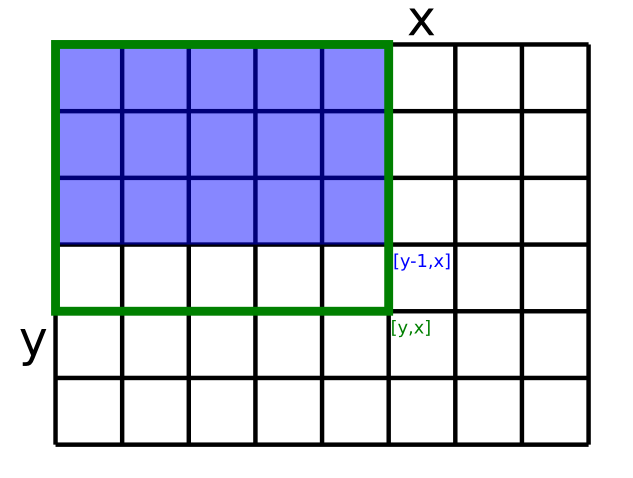
Zároveň je t[y][x] dosť podobné číslu t[y][x-1],
líši sa od neho iba o súčet prvých y čísel v x-tom stĺpci poľa d.
Ak sčítame t[y-1][x] a t[y][x-1] a pripočítame ešte d[y-1][x-1],
dostaneme súčet všetkých čísel v obdĺžniku s y riadkami a x stĺpcami
v ľavom hornom rohu poľa d,
akurát tam niektoré čísla budú zarátané dvakrát.
Konkrétne to budú všetky čísla v obdĺžniku (y−1)×(x−1) v ľavom hornom rohu.
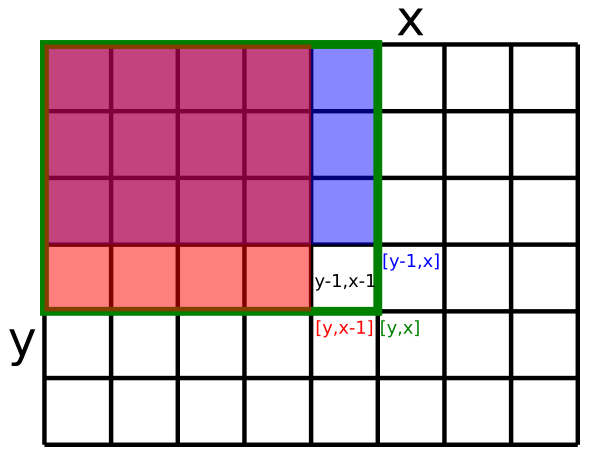
Súčet týchto čísel je vlastne prefixová suma t[y-1][x-1].
Stačí nám túto hodnotu odrátať a dostaneme súčet čísel v obdĺžniku y×x
v ľavom hornom rohu, čo je hodnota t[y][x].
Hodnota t[y][x] teda bude rovná t[y-1][x] + t[y][x-1] + d[y-1][x-1] - t[y-1][x-1].
Pomocou tejto rovnosti môžeme pole t postupne po riadkoch
(zhora nadol, v rámci riadka zľava doprava) vyplniť -- keď budeme vypĺňať t[y][x],
všetky tri čísla t[y-1][x], t[y][x-1] aj t[y-1][x-1] už budeme poznať.
n, m
d = [ [0 for i in range(m)] for j in range(n) ] # vstupne pole
t = [ [0 for i in range(m+1)] for j in range(n+1) ] # pole, kam chceme ulozit prefixove sumy
for y in range(n):
t[y][0] = 0 # nulty stlpec su nuly
for x in range(m):
t[0][x] = 0 # nulty riadok su nuly
for y in range(n):
for x in range(m):
t[y][x] = t[y][x-1] + t[y-1][x] + d[y-1][x-1] - t[y-1][x-1]