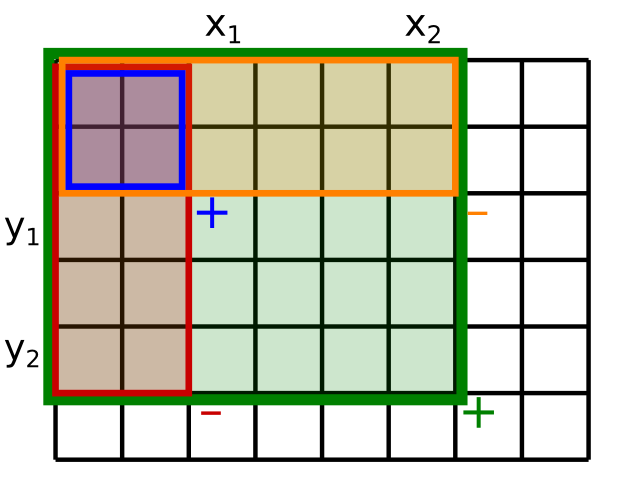
Využitie

Nakoniec si ešte ukážeme, ako s pomocou 2D prefixových súm vieme spočítať súčet čísel v ľubovoľnom obdĺžniku. Povedzme, že chceme spočítať súčet čísel v obdĺžniku, ktorého ľavé horné rohové políčko je d[y_1][x_1] a pravé dolné políčko je d[y_2][x_2]. Prefixová suma t[y_2+1][x_2+1] nám dá súčet všetkých čísel v obdĺžniku s ľavým horným rohom d[0][0] a pravým dolným rohom d[y_2][x_2]. To je väčší obdĺžnik, než sme chceli, preto od neho odrátame obdĺžnik s ľavým horným rohom v d[0][0] a pravým dolným rohom d[y_2][x_1-1], teda prefixovú sumu t[y_2+1][x_1]. Tým dostaneme súčet čísel v obdĺžniku s ľavým horným rohom d[0][x_1] a pravým dolným rohom d[y_2][x_2], čo je ešte stále väčší obdĺžnik, než by sme chceli. Potrebovali by sme ešte odčítať obdĺžnik s rohmi d[0][x_1] a d[y_1-1][x_2]. To nie je žiadna prefixová suma, vieme ho však dostať ako rozdiel t[y_1][x_2+1] - t[y_1][x_1]. Súčet čísel v obdĺžniku s rohmi d[y_1][x_1] a d[y_2][x_2] dostaneme ako t[y_2+1][x_2+1] - t[y_2+1][x_1] - t[y_1][x_2+1] + t[y_1][x_1]. Podobne ako pri jednorozmerných prefixových sumách, ak budeme používať polootvorené intervaly (teda obdĺžnik budeme zadávať súradnicami ľavého horného rohu a súradnicami najbližšieho políčka napravo dole od pravého dolného rohu), výraz sa ešte zjednoduší na t[y_2][x_2] - t[y_2][x_1] - t[y_1][x_2] + t[y_1][x_1].