Fronta (queue)

Rad

Rad (queue alebo aj fronta) funguje presne ako rad v supermarkete pri pokladni. Nový zákazník sa vždy postaví na koniec radu, a pokladníčka vždy obslúži toho, kto je na začiatku. Okrem toho máme k dispozícii ešte jednu operáciu -- môžeme sa pozrieť na to, kto je na začiatku. V súvislosti s radom sa môžeme stretnúť aj s názvom FIFO -- "first in, first out", čiže "prvý dnu, prvý von" (pretože zákazník, ktorý sa do radu postavil ako prvý, bude aj prvý obslúžený).

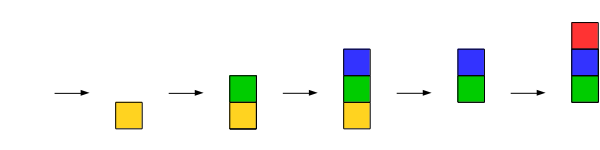
Rad má, podobne ako zásobník, mnoho využití.¹ Môžeme si ním pomôcť napríklad pri implementovaní správania sieťovej tlačiarne -- tá zvláda tlačiť len nejaké množstvo strán za sekundu (povedzme jednu), ale pritom jej môže prikázať tlačiť mnohostranné dokumenty hneď za sebou niekoľko používateľov. V takom prípade si tlačiareň ukladá nové dokumenty do radu a keď dotlačí to, čo mala začaté, pustí sa vždy do toho dokumentu, ktorý čakal najdlhšie (čiže do toho, ktorý prišiel prvý).

Rad je tiež abstraktná dátová štruktúra. Podporuje nasledovné operácie:

• pridať prvok (na koniec),
• odobrať prvok (zo začiatku),
• pozrieť sa na prvý prvok.

Tieto operácie vieme, podobne ako pri zásobníku, implementovať viacerými spôsobmi. Zrejme najintuitívnejší je spájaný zoznam: pamätáme si pointre $prvy$ na prvý a $posledny$ na posledný prvok zoznamu. Keď chceme pridať nový prvok do radu, pridáme ho na koniec zoznamu a aktualizujeme si $posledny$ tak, aby ukazoval na novopridaný prvok. Keď chceme odobrať prvý prvok radu, aktualizujeme $prvy$ tak, aby ukazoval na nasledovníka prvku, na ktorý $prvy$ ukazoval predtým. Keď sa chceme pozrieť na prvý prvok, pozrieme sa na miesto, kam ukazuje $prvy$.

S implementáciou pomocou poľa je to trochu zložitejšie. So zásobníkom to bolo jednoduché preto, lebo jeho "začiatok" -- miesto, kde je uložený najstarší prvok -- sa nehýbal. Rad sa ale hýbe -- predlžuje sa do jedného smeru a skracuje sa z druhého. Čo sa s tým dá robiť? Mohli by sme zakaždým, keď vyberieme prvý prvok z radu, celý rad posunúť. Toto by ale dlho trvalo (pre rad s $n$ prvkami by bolo treba $n$, čiže lineárne veľa, operácií). Naštastie, tento problém vieme vyriešiť malým trikom: namiesto toho, aby sme posúvali rad, posunieme "pokladňu" -- čiže smerník na prvý prvok. (Toto funguje tak, ako keby sme mali pole "zahnuté" do kruhu -- za posledným políčkom nasledujú prvé políčko.) Implementácia teda vyzerá takto: pamätáme si pole $A$ dĺžky $n$, index $zaciatok$ a premennú $k$, v ktorej máme uložené, koľko prvkov je v aktuálne v rade. Keď chceme pridať nový prvok, a platí $k < n$, prvok vložíme na miesto $A[(zaciatok + k) \% n]$² a $k$ zväčšíme o $1$. (Ak $k = n$, tak je pole plné, a nový prvok sa doň už nezmestí.) Keď chceme odobrať prvok, a platí $k > 0$, jednoducho zmeníme $zaciatok$ na $(zaciatok + 1) \% n$ a $k$ zmenšíme o $1$. (Ak $k = 0$, nemáme aký prvok odobrať, lebo rad je prázdny.) Ak sa chceme pozrieť na prvý prvok v rade, pozrieme sa na prvok $A[zaciatok]$.

Obe implementácie majú rovnaké zložitosti. Pamäťová zložitosť celej štruktúry je $n$. Časové zložitosti jednotlivých operácií sú rovnaké -- $O(1)$. (Pre rad platí rovnaká poznámka o časovej zložitosti pridávania prvku ako pre zásobník -- ak budeme mať plné pole, a budeme chcieť jeho obsah prekopírovať do nového, väčšieho poľa, bude to v najhoršom prípade trvať dlho.)