Ďalšie triedenia

V tomto texte opíšeme niekoľko triedení, ktoré sú podobné ako min sort. Skúste si ich naprogramovať na predchádzajúcej úlohe!

Max sort

Triedenie, ktoré ste sa práve naučili (min sort) v každom kroku dalo na začiatok poľa najmenší prvok zo zostávajúceho zvyšku poľa. Samozrejme, veľmi podobne by fungovalo aj triedenie v prípade, že by sme hľadali najväčší prvok a umiestňovali ho na koniec poľa. Skúste si premyslieť, že rovnaká analýza zložitosti by sa dala použiť aj v tomto prípade, a teda aj toto triedenie má zložitosť $O(n^2)$. Ani pseudokód by sa veľmi nezmenil:

def maximum_na_koniec(A, koniec):
  # z prvkov pola A po index `koniec`
  ...
  # vyberie maximum a da ho do pola na index `koniec`

A = [...]
for i in range(n-1, -1, -1):
  maximum_na_koniec(A, i)
print(A)

Insertion sort

Insertion sort je ďalšie známe triedenie. Funguje na základe nasledujúcej myšlienky: Predstavme si, že máme utriedenú nejakú časť poľa, a chceme do tejto časti poľa vložiť ďalšie číslo (označme toto číslo ako x). To vieme pomerne jednoducho: prechádzame pole odzadu, a v momente ako nájdeme prvé číslo menšie alebo rovné ako x, tak vieme, že x by sme mali do poľa "vložiť" za toto miesto.

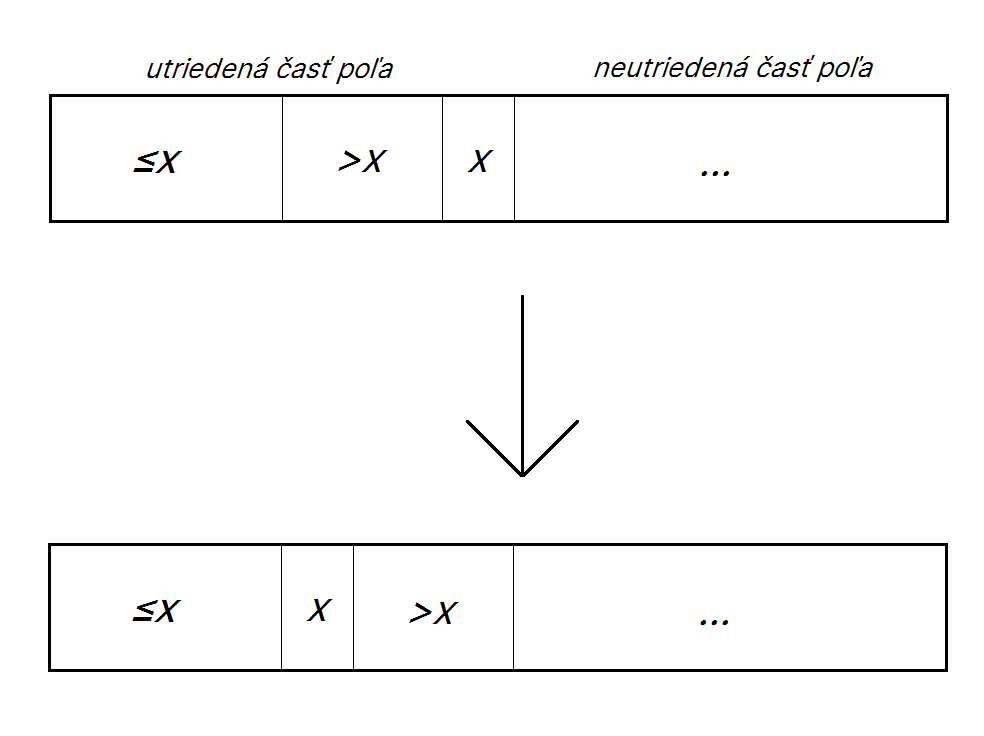
Do poľa ale nevieme len tak jednoducho "vložiť" prvok na nejaký index, takže musíme prvky, ktoré sú napravo "poposúvať", by sme na prvok x "urobili miesto". Keď je prvok x na správnom mieste, máme o 1 prvok väčšiu utriedenú časť poľa. Takto môžeme pokračovať, až kým nie je celé pole utriedené. Toto posúvanie sa najjednoduchšie realizuje už priamo pri hľadaní miesta, kam máme x vložiť tak, že postupne vymieňame prvky ako to miesto hľadáme.

Odkiaľ ale takéto triedenie začať? Ako získame to počiatočné utriedené pole? Veľmi jednoducho, keďže 1 prvkové pole je utriedené vždy, tak môžeme začať odtiaľ.

A = [...]
for i in range(1, n):
  x = A[i]                     # x je prvok, ktory vkladame
  for j in range(i-1, 0, -1):  # nájdem, kam prvok A[i] patrí
    if A[j-1] > A[j]:
      # vymeň A[j] a A[j-1]
    else:                      # už sme našli správne miesto na prvok x
      break

print(A)

Časová zložitosť tohoto triedenia je tiež $O(n^2)$, keďže na správne miesto potrebujeme umiestniť $n$ prvkov a kvôli prvému z nich potrebujeme premiestniť najviac $1$ prvok, kvôli druhému $2$ prvky, kvôli tretiemu $3$ prvky, ..., kvôli poslednému ($n$-tému) najviac $n$ prvkov.

A ak si spomínate, v analýze zložitosti min sortu sme sumu $1+2+3+\dots+n$ už videli. Rovnako ako v prípade min sortu je teda výsledná zložitosť $O(n^2)$.

Bubble sort

Posledným triedením, ktoré v tomto texte spomenieme je bubble sort. Je viac variant, ktoré sa môžu líšiť v zložitosti v prípade, že je pole, ktoré triedime nejakým spôsobom "takmer utriedené" (napríklad je najväčší prvok na začiatky, ale inak sú všetky prvky utriedené správne).

Najjednoduchší kód ale vyzerá tak, že jednoducho $n$ krát porovnáme všetky susedné prvky a v prípade, že nie je ľavý menší ako pravý, tak ich vymeníme.

A = [...]
for i in range(n):
  for j in range(1, n):
    if A[j-1] > A[j]:
      # vymeň A[j] a A[j-1]

print(A)

Z kódu je asi jasné, že časová zložitosť programu je $O(n^2)$. To čo ale asi nie je jasné, že prečo by malo triedenie fungovať. Skúste si to premyslieť. Hint: predstavte si, čo sa udeje napríklad s najväčším prvkom v poli po jednom behu vonkajšieho cyklu (a ako veľmi to závisí od toho, kde sa ten prvok na začiatku triedenia nachádzal).