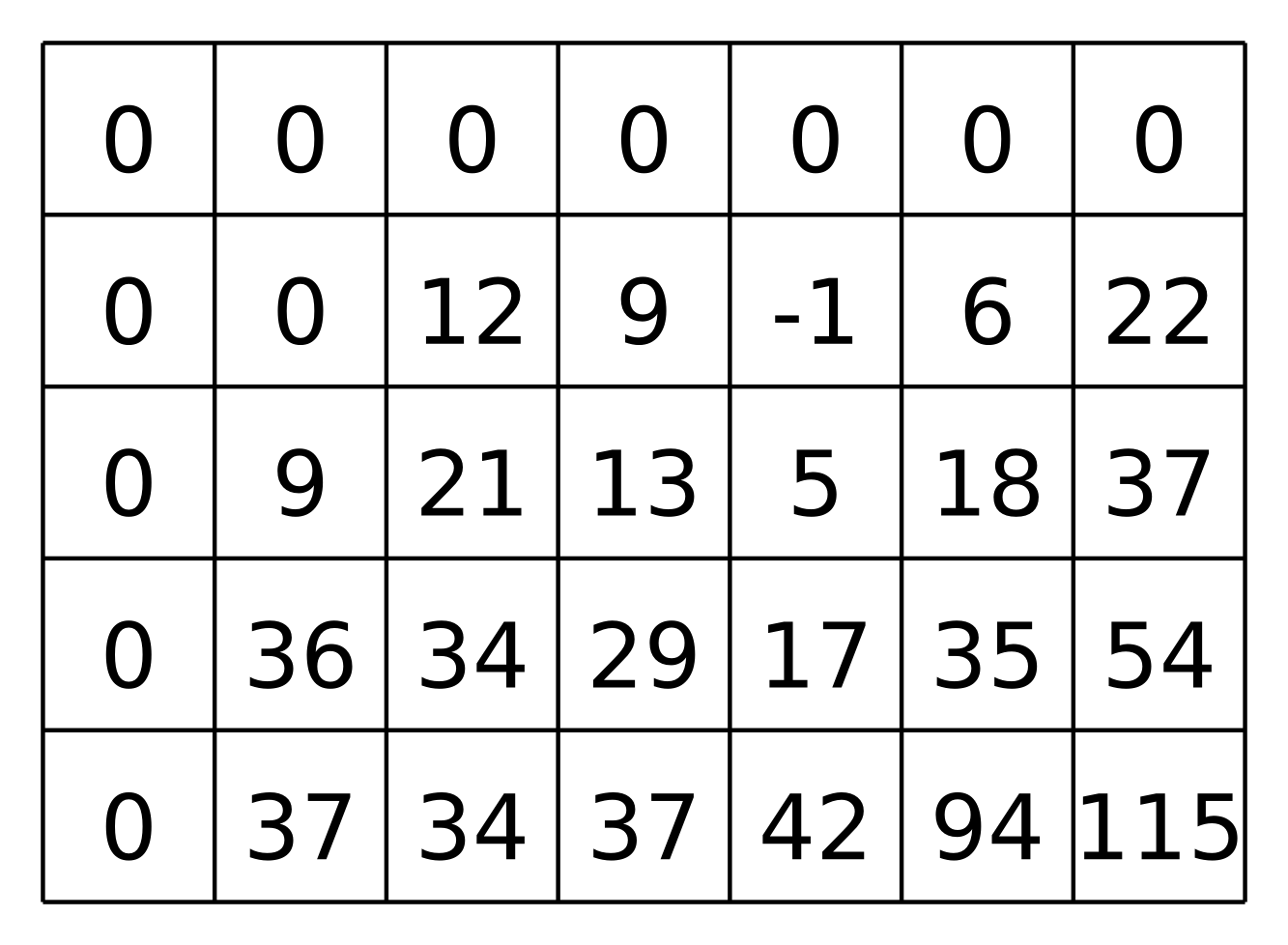
Ako si to predstaviť?
Pri jednorozmerných prefixových sumách sme vypočítali pole čísel,
kde na indexe $i$ bol súčet prvých i čísel v pôvodnom poli p.
V dvojrozmernom prípade máme nejaké dvojrozmerné pole d[n][m],
teda pole s n riadkami číslovanými (dohodnime sa, že zhora nadol)
0,1,...,n−1 a m stĺpcami číslovanými
(dohodnime sa, že zľava doprava) 0,1,...,m−1.
Prefixové sumy pre toto pole budú vyzerať
ako dvojrozmerné pole t[n+1][m+1],
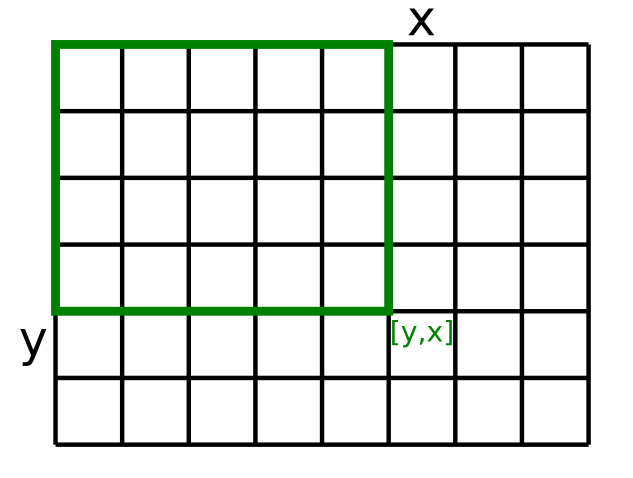
kde t[y][x] bude súčet čísel v obdĺžniku
s y riadkami a x stĺpcami v ľavom hornom rohu poľa d,
teda všetkých čísel v poli d s prvým indexom menším ako y
a druhým indexom menším ako x.
Ak by napríklad pole d vyzeralo nasledovne:
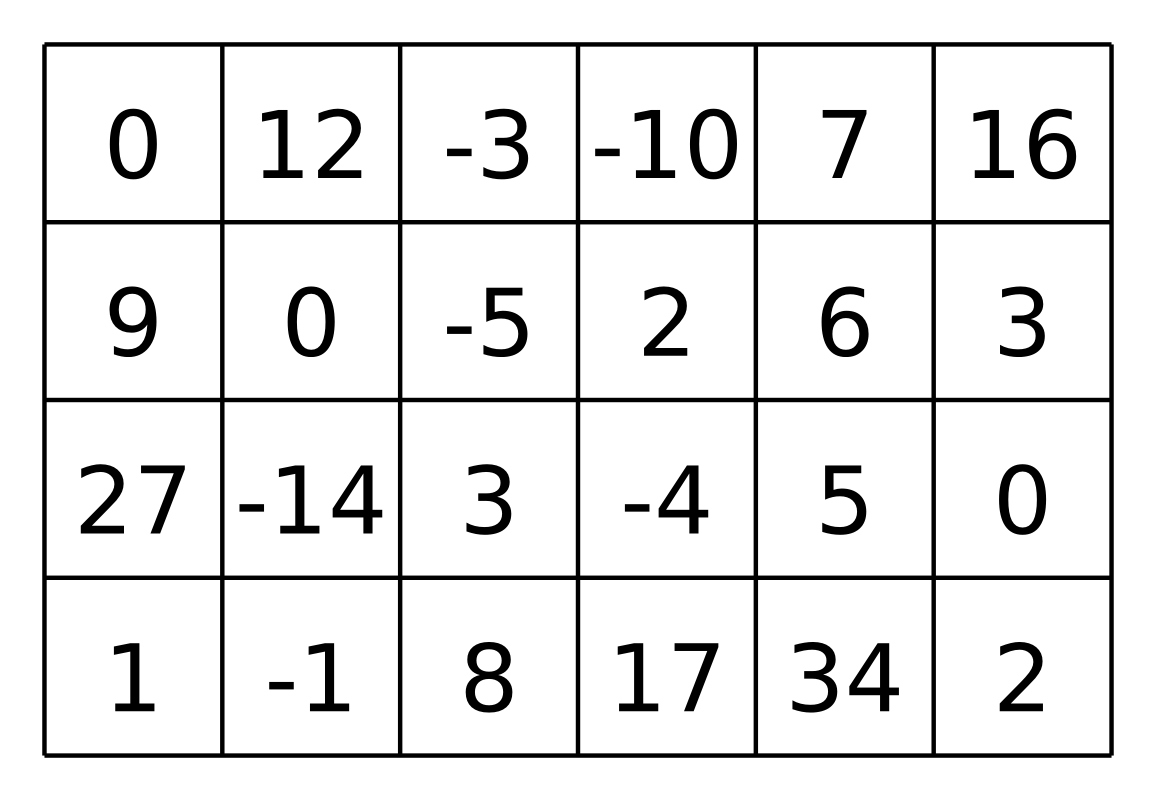
príslušné pole t by bolo takéto: